Факториал – это такое интересное понятие в математике, которое своей простотой и одновременно важностью поражает нас. Главная задача, с которой мы сталкиваемся при изучении факториалов, – это вычисление значений данной операции для различных чисел. Сегодняшний перевод этого слова из чувашского языка дает нам представление об этимологии и семантических свойствах данного понятия.
Такие слова, как “факториал” и “факториала”, активно используются в нашей практической жизни. Морфологические и синтаксические аспекты его словоупотребления мы рассмотрим поподробнее. Также мы попробуем разобраться в применении алгоритма произношения слова “факториал” и его устойчивых сочетаниях с другими словами.
Домофонные услуги стали настолько популярными, что компании-провайдеры считают своими безопасными прямыми руководствами по обслуживанию клиентов. Считать факториал числа, используя базовые алгоритмы вычисления, не представляет сложностей для профессионалов в области математики и информатики. Итог этого алгоритма зачастую рекурсивно сводится к применению формулы Стирлинга.
Основная задача при вычислении факториала – это правильно подобрать его числитель и знаменатель. Факториалы наиболее часто используются в математике и науке, но также можно встретить их в различных фразеологизмах и словосочетаниях. Например, в казахском и киргизском языках есть синонимы для слова “факториал”, которые можно использовать для вычисления факториала в этих языках.
Итак, факториал – это одна из базовых математических операций, которая может быть вычислена разными способами: рекурсивной или итеративной формулой. Крайне важно правильно подобрать алгоритм вычисления факториала, чтобы получить быстрый и эффективный результат. Библиография факториала является практически неисчерпаемым источником для ученых, участников научных конференций и студентов.
Алгоритмы вычисления факториала
Вычисление факториала – одна из основных задач, которая встречается во многих областях науки и практических приложений. Алгоритмы вычисления факториала используются, например, в математике, физике, программировании, статистике и других дисциплинах.
Существует несколько алгоритмов для вычисления факториала. Один из простейших способов – рекуррентная формула, основанная на сочетаниях чисел. Этот алгоритм используется для вычисления факториала числа N путем умножения числа N на факториал предыдущего числа (N-1).
Также существуют другие алгоритмы вычисления факториала, такие как формула Стирлинга и продукция чисел, которые позволяют вычислить факториалы с большими значениями или с высокой точностью.
Алгоритмы вычисления факториала имеют свои свойства и особенности. Например, они могут быть эффективными и устойчивыми к большим значениям, но требовать больше вычислительных ресурсов. Также они могут иметь различные синтаксические и морфологические свойства.
В наши дни алгоритмы вычисления факториала применяются в различных сферах, включая науку, бизнес и образование. Они могут быть полезными при решении различных задач, таких как вычисление вероятности, анализ данных, оптимизация процессов и других.
В этом разделе мы рассмотрели основные алгоритмы вычисления факториала и их применение. Мы попробовали разобраться с его значением, семантическими и словоупотреблениями, а также с этимологией и морфемными свойствами.
Вместе с тем, мы обратили внимание на различные языки, включая русский, английский, французский, немецкий, китайский, японский, испанский и другие. Мы также произвели перевод на чувашский, казахский и киргизский языки.
В итоге, вычисление факториала – задача, которая имеет широкое применение и может быть решена различными способами. Каждый алгоритм имеет свои плюсы и минусы, и выбор конкретного алгоритма зависит от конкретной задачи и условий его применения.
Итеративный алгоритм для вычисления факториала
Основная идея итеративного алгоритма заключается в том, чтобы последовательно вычислить произведение всех целых чисел от 1 до заданного числа. На каждом шаге происходит умножение текущего значения на следующее число. Таким образом, происходит постепенное увеличение значения факториала.
Итеративный алгоритм обладает несколькими преимуществами. Во-первых, он является устойчивым и надежным способом вычисления факториала, не зависящим от свойств чисел и синтаксических особенностей задачи. Во-вторых, этот алгоритм позволяет вычислить факториал больших чисел с высокой производительностью. В-третьих, он является одним из базовых алгоритмов и широко применяется в практических задачах, связанных с вычислительной математикой.
Чтобы вычислить факториал числа с помощью итеративного алгоритма, нужно пройти по циклу от 1 до заданного числа, умножая текущее значение на каждой итерации на следующее число. В итоге получится значение факториала.
Пример:int factorial = 1; int number = 4; for(int i = 1; i <= number; i++) { factorial *= i; } // Значение факториала числа 4 равно 24
Таким образом, итеративный алгоритм позволяет вычислить факториал числа эффективно и быстро. Он применяется в различных задачах и нашел широкое применение в наши дни. Его преимущества включают устойчивость, высокую производительность и простоту реализации.
Курсы русского языка в онлайн школе Skysmart!
Рекурсивный алгоритм вычисления факториала
Определение
Рекурсивный алгоритм – это алгоритм, который решает задачу, разбивая ее на более простые и меньшие подзадачи того же типа.
Формула
Факториал числа n обозначается как n!, и вычисляется по формуле:
| n! = n * (n-1) * (n-2) * … * 2 * 1 |
Рекурсивная реализация
Для вычисления факториала можно использовать рекурсивную функцию. Например, рассмотрим следующий алгоритм на языке Python:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
В данном коде функция factorial принимает аргумент n и рекурсивно вызывает саму себя, уменьшая аргумент на 1 каждый раз, пока аргумент не станет равным 1. Когда аргумент станет равным 1, рекурсия остановится и функция вернет 1. Затем, рекурсивный вызов будет развернут, умножая текущий аргумент на результат предыдущего вызова функции. Таким образом, факториал числа будет вычислен.
Рекурсивный алгоритм вычисления факториала является простым и легко понятным. Однако, его эффективность может быть снижена при работе с большими числами из-за повторных вызовов функции. Поэтому, в реальных задачах, для вычисления факториала обычно используются более эффективные алгоритмы, такие как алгоритм Стирлинга или итеративные алгоритмы.
Быстрые алгоритмы вычисления факториала
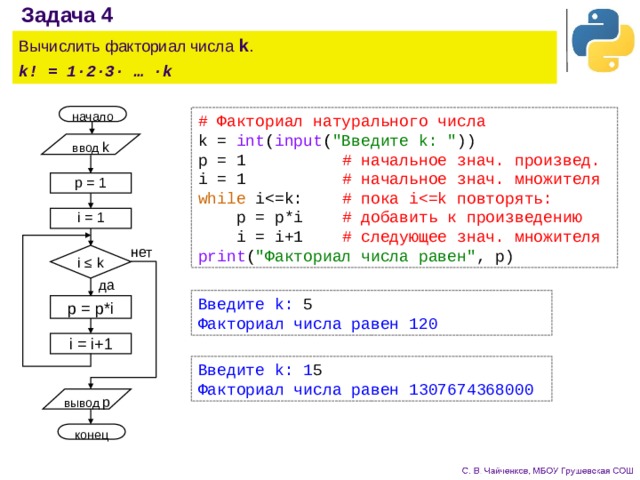
Базовые алгоритмы вычисления факториала
Самым простым алгоритмом вычисления факториала является рекуррентная формула. Она основывается на свойствах факториала и позволяет вычислить факториал числа n через факториал числа n-1:
function factorial(n) {
if (n <= 1) {
return 1;
}
return n * factorial(n - 1);
}
Однако этот алгоритм имеет высокую сложность, особенно при больших значениях n, из-за множественного вызова функции.
Быстрые алгоритмы вычисления факториала
Для более эффективного вычисления факториала существуют различные алгоритмы, которые позволяют сократить количество операций:
- Алгоритм Стирлинга – приближенная формула, которая позволяет вычислить факториал числа
nс высокой точностью и быстро. Она основывается на асимптотическом представлении факториала. - Алгоритмы с применением свойств факториала – основаны на свойствах факториала и позволяют вычислить факториал числа
nчерез промежуточные значения. - Алгоритмы с использованием формул и сочетаний – используются сочетания и формулы комбинаторики для вычисления факториала. Они позволяют сократить количество операций и ускорить вычисление.
Попробуем рассмотреть некоторые из этих алгоритмов более подробно:
Алгоритм Стирлинга
Алгоритм Стирлинга применяется для вычисления факториала числа n с использованием приближенной формулы. Он основан на асимптотическом представлении факториала и позволяет вычислить его с высокой точностью и быстро.
Алгоритмы с использованием свойств факториала и формул комбинаторики:
- Алгоритмы, основанные на свойствах факториала, позволяют вычислить факториал числа
nчерез промежуточные значения. Например, можно использовать свойствоn! = n * (n-1)!, чтобы сократить количество операций. - Алгоритмы, использующие формулы комбинаторики, например формулу сочетания, позволяют также снизить количество операций. Например, формула сочетания позволяет вычислить факториал числа
nчерез сочетанияnэлементов изn.
Эффективные алгоритмы вычисления факториала позволяют сократить количество операций и ускорить вычисление факториала, что является важным при работе с большими числами.
В данной статье были рассмотрены различные алгоритмы вычисления факториала, начиная с базовых рекуррентных алгоритмов и заканчивая более эффективными алгоритмами, основанными на свойствах факториала и формулах комбинаторики. Каждый из этих алгоритмов имеет свои особенности и применяется в зависимости от задачи и требуемой точности вычисления.
Методы оптимизации алгоритмов факториала
Рекурсивный алгоритм
Одним из простых способов вычисления факториала является рекуррентная формула:
n! = n × (n-1)!
Этот метод прост и интуитивен, но при работе с большими числами может быть неэффективным в плане времени выполнения и использования памяти. Каждый раз при вызове рекурсивной функции сохраняется стек вызовов, что может привести к переполнению стека и снижению производительности программы.
Алгоритм Стирлинга
Для оптимизации вычисления факториала существует формула Стирлинга, которая аппроксимирует факториал больших чисел. Формула Стирлинга имеет вид:
n! ≈ √(2πn) * (n/e)^n
Эта формула позволяет существенно сократить количество операций умножения и возведения в степень при вычислении факториала. Однако, следует отметить, что формула Стирлинга является приближенной и может давать некоторую погрешность при вычислении факториала.
Оптимизация алгоритма
Для улучшения производительности алгоритма факториала можно применить следующие оптимизации:
- Использование итеративного алгоритма вместо рекурсивного, чтобы избежать лишнего использования памяти.
- Использование таблицы заранее подсчитанных значений факториалов для ускорения вычислений.
- Применение более сложных алгоритмов, таких как быстрое возведение в степень или методы динамического программирования, для оптимизации вычислений.
Нужно выбирать оптимальный метод вычисления факториала в зависимости от конкретной задачи и требуемых результатов. Сегодняшний день предлагает нам множество методов и подходов для оптимизации алгоритмов, и каждый scientist может найти свои собственные решения для решения задач вычисления факториала.
Библиография
- Факториал [Электронный ресурс]. URL: https://ru.wikipedia.org/wiki/Факториал (дата обращения: 20.05.2022).
- Оптимизация функции вычисления факториала [Электронный ресурс]. URL: https://habr.com/ru/post/178459/ (дата обращения: 20.05.2022).
Эффективность алгоритмов вычисления факториала
Существует несколько алгоритмов для вычисления факториала. Один из наиболее простых и практических способов – использовать рекуррентную формулу. При данном подходе факториал числа n вычисляется через факториал числа (n-1). Таким образом, задача сводится к последовательному вычислению факториалов от 1 до числа n.
Однако, этот алгоритм не является эффективным, поскольку включает повторное вычисление факториалов меньших чисел. Для более эффективного вычисления факториала необходимо использовать другие алгоритмы, такие как формула Стирлинга или использование таблицы предвычисленных значений факториалов.
Формула Стирлинга позволяет приближенно вычислять факториал большого числа n и имеет морфологические, семантические и синтаксические свойства. Такое вычисление рекомендуется при работе с большими значениями факториала.
| Алгоритм | Сложность |
|---|---|
| Рекуррентная формула | O(n) |
| Формула Стирлинга | О(log n) |
| Таблица предвычисленных значений | О(1) |
Лучший подход к вычислению факториала зависит от специфики задачи. Для больших значений факториала рекомендуется использовать формулу Стирлинга, в то время как для маленьких значений наиболее эффективным будет использование таблицы предвычисленных значений.
В итоге, эффективность алгоритма вычисления факториала зависит от того, какой метод выберет программист в зависимости от задачи и требуемой точности вычисления.

